タイヤの太さと摩擦力の関係

2021年2月11日2021年2月12日

タイヤが太くなっても摩擦力が変わらないって本当？

タイヤが太くなっても摩擦力が変わらないという話があります、これは本当なのでしょうか？
なんとなく体感的に思うのは太い方が摩擦力あるように感じるし、太いタイヤは押し引きも重いのでそうなんじゃないの？とか思ってしまいますが。

細いタイヤでもグリップしていた？

こんな話があります、ジムカーナライダーのコンバット氏は以前ジムカーナマシンのKSR110のリアタイヤにフロントタイヤを履かせて競技に参加してトライジムカーナ大会で見事総合優勝を果たしたことが有ります。
異様に細いリアタイアでしたが抜群に速く、本人に問題ないの？と聞いてみましたが、特に問題は無かったとのこと、切り返しが異様に早いらしく並大抵の腕では使いこなせそうに無い気もしますが、グリップ力に不足は感じなかったそうな。
ジムカーナ界隈ではたまにミニバイクや軽量な小排気量マシンで稀にフロントタイヤをリアに仕込むことを試す方がいらっしゃいます、私の知る限りではもう一人試してた方がいらっしゃいます。
あと、バイクではないのですが昔ラジコンカーをやっていた時、当時ゴムタイヤのトレッド幅は26ミリだったんですが、そこにあるドライバーがトレッド幅を20ミリにまで詰めて自作した人が居てそれが無茶苦茶速くて話題になりあっという間に流行った事が有ります、そのあまりにも細いタイヤは見た目がカッコ悪いと嫌う人もいましたが、使ってみた事ありますが、グリップは落ちているという感じは無く、機敏に反応するので速かったのは確かですね、反面ややローグリップな路面ではシビアな挙動があったと記憶していますがずいぶん昔ですし、当時はタイヤの種類も限られてたので。
その後スーパーナローと呼ばれたこのタイヤはレギュレーションで禁止されて現在は24ミリ幅のミディアムナロータイヤが主流となっていますが。
まぁ同条件で比較して無いのでこれだけではグリップが変わらないという根拠にはなりませんが。

タイヤが太くても摩擦力が変わらないという考えの根源

この考えの根源にあるのは高校の物理などで習う摩擦力の公式アモントン・クーロン則
F=μN（μ：摩擦係数、N：垂直荷重）
というのが有ります、これには接地面の面積が含まれていない為太くして接地面積を増やしてもその分荷重が分散されて減るので変わらないという訳ですね。
この法則は広い範囲において成立する法則なのですが、この法則が万能かというとそうでも無くてこの法則に破れが生じる例はいくつか発見されています、一番わかりやすい例は境界面に液体などが存在するとこの法則は当てはまらなくなります、そして今回の話題のゴムなどの弾性体でもこの法則に破れが生じる事がわかっています。

タイヤの摩擦力の正体って何？

では、タイヤの摩擦力の正体って何でしょう？実のところよく分かってないんです、多分これだというのは推測されていて、それは凝着（粘着？）摩擦とヒステリシス摩擦の足しあわされたものががゴムの摩擦力と推測されています。
ゴムの摩擦力F=F adhesion＋F hysteresis（F adhesion：凝着摩擦、F hysteresis：ヒステリシス摩擦）で表されます、まず凝着摩擦ですが
F adhesion＝tAr（t：せん断強さ、Ar：真実接触面積）で表されます。
凝着とは接触面はミクロで見れば凹凸があり、その一部が接触しているわけですがその接触部がくっ付こうとする性質が凝着で、それを引きはがそうとするのがせん断です、そのせん断に対する強さがせん断強さで真実接触面積はゴムと路面同士が分子的に接触している面積になります。
そしてヒステリシス摩擦は粘弾性特性によって生じる摩擦力で、粘弾性とはばねのように物体が変形した量のみに依存した力ではなく、ダンパーのように変形する速度にも依存して力を発生させるという特性なんですが、分かり難いと思います。

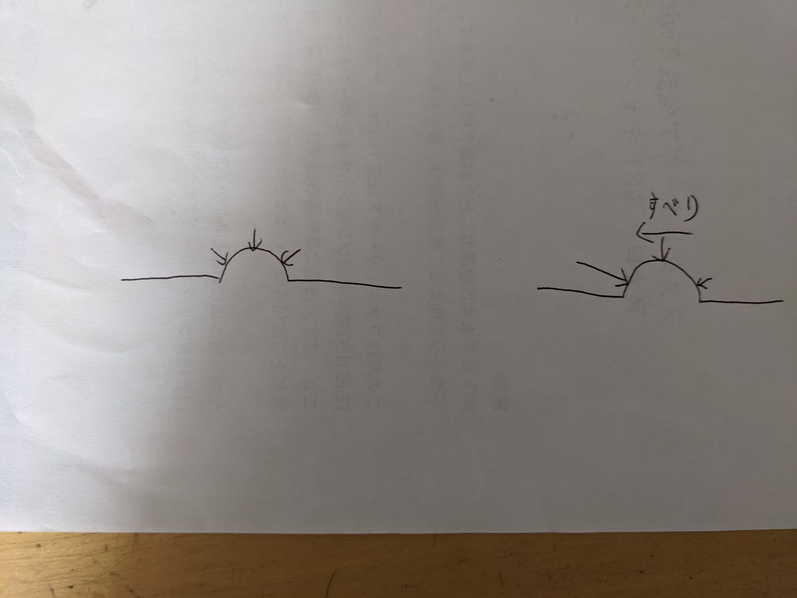
この図を見て欲しいのですが（汚い図ですまんです）、左は静止している図右は左に滑りを生じている図です、静止している場合は突起に対して変形してそれに対して均等に力を返しますが、ここに滑りが生じるとゴムの粘弾性で力が抜ける側（右側）のゴムの反力が弱くなりより左側の押し返す力のほうが大きくなる為、抵抗を生じます、これがヒステリシス摩擦になります。
これはある程度の速度と滑りが発生している状況の時に大きくなると考えられます、やや滑りが生じているときにグリップが最大になるのはこの辺が要因なのではと思います。

荷重と摩擦力の関係

ここが重要なんですが、荷重と摩擦力の関係を今までのF=μNで考えると、荷重が大きくなると摩擦力もいくらでも大きくなるのですが、現実世界ではそうならないんですね。
実際には荷重と摩擦力はある程度のところまで行くと比例関係ではなくってしまいます、良くサチュレートとか飽和すると言ったりしますが、つまり荷重が増加しても摩擦力はあまり大きくならなくなっていきます。
その理由は、真実接触面積の荷重が比較的小さい段階では荷重の増加とともに接触部分が変形し、凝着する面積が大きくなるのですが、荷重がある程度以上大きくなると凝着部分はすでに変形が進行しているので、それ以上の荷重が増えても凝着面積が増加しなくなってきます、つまり外力に対するせん断強さも増加せず、摩擦力が増加しなくなってきます。
荷重と摩擦力の関係が荷重の増加とともに比例関係を失うのはこういう理由からです。

タイヤを太くするとグリップ限界が上がる理由

結論から言うとタイヤ幅を太くして、荷重と摩擦力が比例関係を保つ荷重領域を増やすことでグリップ限界を上げているから。
つまり太くても細くてもある程度の荷重域までは比例関係で荷重に合わせてグリップが増しますがタイヤを太くしてやると荷重が分散されてより大きな荷重でも比例して摩擦力が増える為太いとグリップが上がる訳です。
なので、太くしたらグリップ限界は上がりますがその領域までいかないのであれば太くても意味ないどころか重くなったり、バイクならバンクさせ辛くなったりといったデメリットも有る訳です。
なので例に挙げたフロントタイヤリアに履かせるとか細いタイヤで速かったというのは有りうるわけですが、純粋にグリップ限界だけで語れないのが難しい話でして、その分動きが早くなって操作がシビアになったり、細いタイヤは面圧が上がる分摩耗も早くなります、レースマシンのタイヤが太いのは耐久性を上げるといった側面も持ち合わせていたりするんですね、要は何事も過ぎたるは及ばざるがごとしで太くても細くても良くないことは有るし丁度いいバランス点があるという事ですね。